Regularization(정규화)
input-output pair를 이용해 모델을 훈련시키는 supervised learning은 input으로 부터 output의 패턴을 정의하는 것입니다. 충분한 양의 데이터로 부터 유의미한 특징을 도출해내어 Error Risk Minimization(ERM) 알고리즘을 이용해 모델을 훈련시키는 방법론은 ML World에서 상당히 지배적인 위치를 차지하고 있었습니다. 많은 양의 데이터가 사람의 손에 의해 라벨링이 되어 네트워크를 충분히 학습시킬 수 있는 대용량 데이터셋들의 등장(예, ImageNet) 은 supervised learning이 인간의 능력을 뛰어넘을 수 있었던 이유 중 가장 중요했던 부분이라고 생각합니다.
하지만, 현실 세계(Real-World)에서는 양질의 데이터를 획득하기 어려울 뿐 아니라, input-output mapping을 유일하게(unique)만들 수 있는 상관관계를 도출해내는 것은 불가능할 수 도 있습니다. 예를 들어, 사람에 의해 라벨링 된 데이터가 중복되어 존재할 수 있고, 정답 라벨(Golden standard)이 아닐수도 있으며, 이상치(outlier) 등 에 의해 머신러닝 모델은 overfitting 또는 underfitting등의 현상이 발생할 확률이 높습니다. 때로는, 훈련데이터의 distribution이 real-world의 distribution을 따르지 않아 생기는 generalization 문제도 종종 발생합니다.
잘못되거나 지나치게 편향된 데이터의 학습으로 부터 overfitting을 막기 위한 방법론으로는 Regularization 이 있습니다. 훈련데이터로 부터 Empirical risk 를 최소화 시키는 방향으로 학습하되, 정규화 Term을 추가로 이용하여 loss landscape를 부드럽게 (Smooth) 해주도록 유도합니다.
Regularized cost function = Empirical cost function + (Regularization parameter) x Regularizer
Regularization term에는 크게 두 가지 방법론이 있습니다.
1. Classical Regularization theory : 우리가 흔히 아는 L1, L2 weight decay를 통해 cost function에 정규화 과정을 적용하여 classifier의 복잡도(complexity)를 조절해주어 ambient space상에서 정규화를 달성할 수 있는 방법론
2. Generalized regularization theory : Classical Regularization theory 를 일부 확장시킨 정규화 방법으로, manifold regularizer라고도 불립니다. 입력 분포의 기하학적 복잡도를 조절해주는 Term을 추가하여 semi-supervised learning의 수학적 근거를 제공해주는 이론입니다.
Semi-Supervised Learning(준지도 학습)
Semi-Supervised Learning(SSL) 이란, 적은양의 labeled data 와 많은 양의 unlabeled data 을 이용해 ML World의 문제를 풀어내는 접근법을 의미합니다. 인간은 한 번도 보지못한 사물일지라도 경험에 의존하여 이전에 본 사물을 바탕으로 새롭게 인식된 사물이 무엇인지 추론합니다. 예를 들어, 오른쪽 이미지의 고양이 사진을 보고 고양이를 알아차린 인간은, 비록 종과 색깔이 다르고 하는짓도 매우 특이하지만(?) 오른쪽 이미지를 고양이라고 인식할 수 있습니다. 왜냐하면, 확실히 정의내릴 수는 없지만 두 사진은 고양이로 인식될 수 있는 많은 특징점들을 공유하고 있기 때문입니다. 이러한 가정(Assumption)을 바탕으로, SSL에서는 적은 양의 Labeled data와 많은 양의 Unlabeled data가 서로 식별 가능한 관계가 있다고 가정하고 이를 찾아내어 모델의 성능을 향상시킬 수 있는 알고리즘 방법론을 찾는 것을 목표로 합니다.

Input data ${x}^N_{i=1}$ 가 주어졌을 때 준지도학습에서는 입력 데이터는 $d$ 라는 라벨의 존재 유무에 따라, Labeled dataset $\{{x}^K_{i=1}, d^K_{i=1}\}$ , Unlabeled dataset $\{{x}^U_{j=K+1}\}$ (d is unknown) 으로 나뉩니다. 따라서, 준지도학습은 supervised learning과 unsupervised learning의 중간 레벨 정도의 학습 이론이라고 볼 수 있습니다.
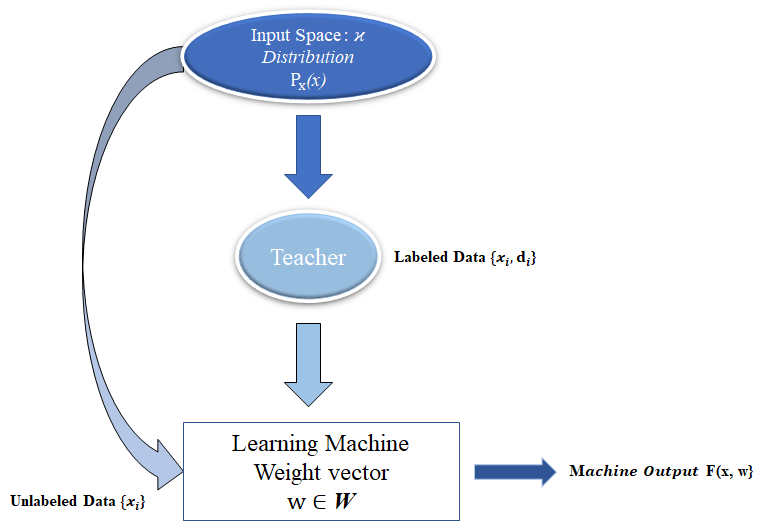
Input space ϰ(should be stationary)가 주어졌을 때, Label data와 Unlabel data를 동시에 이용하여 Machine을 훈련시키는 방법론입니다. Learning Machine은 2개의 subset data로 부터 온 입력값을 받아 output을 생성합니다.
Labeled data $\{{x_i, d_i}\}$ 는 input space ϰ 로 부터 데이터를 샘플링($x_i$)하고 Teacher로 부터 라벨($d_i$) 를 받아 joint distribution을 생성합니다.
$$p_{X,D}(x,d) = p_{D|X}(d|x)p_x(x)$$
$p_{X,D}(x,d)$ 은 라벨링 정보로 부터 오는 Joint Distribution 이고 $p_X(x)$ 는 marginal distribution 입니다. 그에 반해 Unlabeled data $\{x_j\}$ 는 Input space ϰ로 부터 바로 샘플링 받아 모델 훈련에 기여하게 됩니다.
labeled data $p_{X,D}(x,d)$ 와 marginal distribution $p_x(x)$ 에서 샘플링하는 unlabeled data 간의 식별가능한 특정한 Relationship이 존재할 것이라고 가정하고 훈련을 진행하게됩니다. 예를 들어, Labeled data에는 고양이 이미지가 여러개 있기 때문에 이 정보를 바탕으로 Unlabeled data의 고양이 이미지들을 분류해낼 수 있도록 하는 이론적 배경입니다.
두 개의 data point $x_i$, $x_j$ $\in X$ 가 input space ϰ 상에서 매우 가깝게 위치한다면, SSL 은 function F($\cdot$)을 통해 F($x_i$) 와 F($x_j$) 값이 높은 likelihood로 Hypothesis space 상에 가까운 위치에 놓여있다.
위 가정은 SSL의 가정 중 cluster assumption의 내용으로 unlabeled data를 생성하는 marginal distribution $p_x(x)$ 의 특정한 포인트에서 샘플링 된 입력 값들이 같은 "cluster"에 위치한다면 같은 클래스 또는 라벨을 가지게 될 확률이 높다라는 내용입니다. 이외에도 Manifold assumption, Smoothness assumption, Low-density assumption 등이 있지만, Cluster assumption은 위 가정들의 Generalzation version이라고 생각하실 수 있습니다. 그 이유는 모든 Assumption들이 Space 상에서의 Point값들의 유사도(Similarity)를 정의하는 방법론들로 정의될 수 있습니다. 예를 들어, low-density assumption은 high-density area에 있는 두 샘플이 유사하다면 같은 라벨을 갖는 것으로 볼 수 있으며, manifold assumption에서 같은 low-dimensional manifold에 위치한 샘플은 유사하다고 가정합니다. 따라서, SSL assumption은 cluster assumption을 구체화한 가정법들이라고 생각하실 수 있습니다.
이러한 assumption을 만족시키기 위해 또다른 panelty term을 추가해야합니다. 추가적인 term을 통해 달성하고자 하는 것은, 위에서 설명한 Cluster assumption이 만족할 수 있도록 unlabeled data를 처리해주는 것입니다. 예를 들어, Least-Square cost function 아래에서 SSL의 목표를 달성하기 위해, 함수 F$(\cdot)$ 을 이용해 Loss function을 정규화시키는 Term을 아래와 같이 정의하였습니다.

$\lambda_A||F||^2_K$ 의 경우 RKHS 상에서 weight decay 등을 적용하여 labeled set에 대해 classifier의 복잡도를 줄일 수 있는 앞서 설명한 "Classical Regulraization Theory" term 이며, $\lambda_I||F||^2_I$ 는 unlabeled set의 cluster assumption을 만족시키기 위해 input space $p_X(x)$의 intrinsic geometric structure 를 조절해주는 term입니다. 새롭게 정의된 intrinsic geometric structure term을 통해 semi-supervised learning에서는 label-unlabel data 모두가 training algorithm에 기여하도록 만듭니다. 이 추가적인 term 이 가져오는 결과를 알아보기 위해 간단한 실험을 살펴보겠습니다.
1. Intrinsic regularization parameter $\lambda_I$ = 0
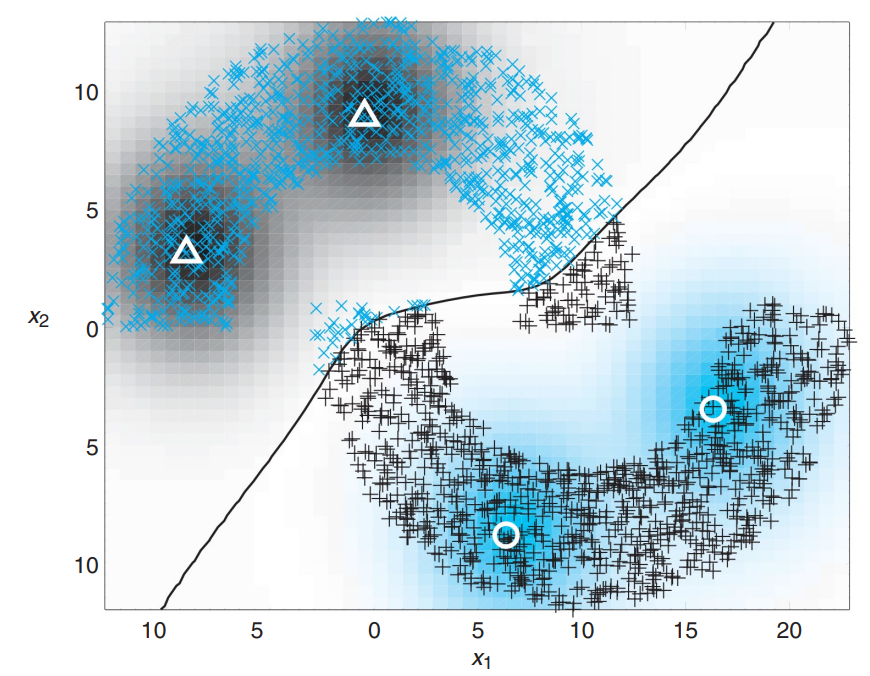
unlabeled data를 전혀 사용하지 않은 채로 labeled data로 훈련을 시킨 경우 decison boundary가 1자 형태를 보여줍니다. 즉, 두개의 클러스터를 만들기 위해 모델 F$(\cdot)$ 은 unlabeled data를 전혀 사용하지 않았기에 많은 양의 데이터가 mislcassification 된 것을 볼 수 있습니다. 또한 데이터의 중간을 가르는 decision boundary가 linear한 형태를 띄고 있음을 알 수 있습니다.

2. Intrinsic regularization parameter $\lambda_I$ = 0.0001
아주 작은 수치를 적용하여 unlabeled data로 부터 decision boundary의 기하학적 구조 변형을 강제하였습니다. 비록 적은 양의 contribution이였지만, 선형 decision boundary가 바뀌었고 오분류된 sample의 수도 눈에 띄게 줄어든 것을 확인 할 수 있습니다.
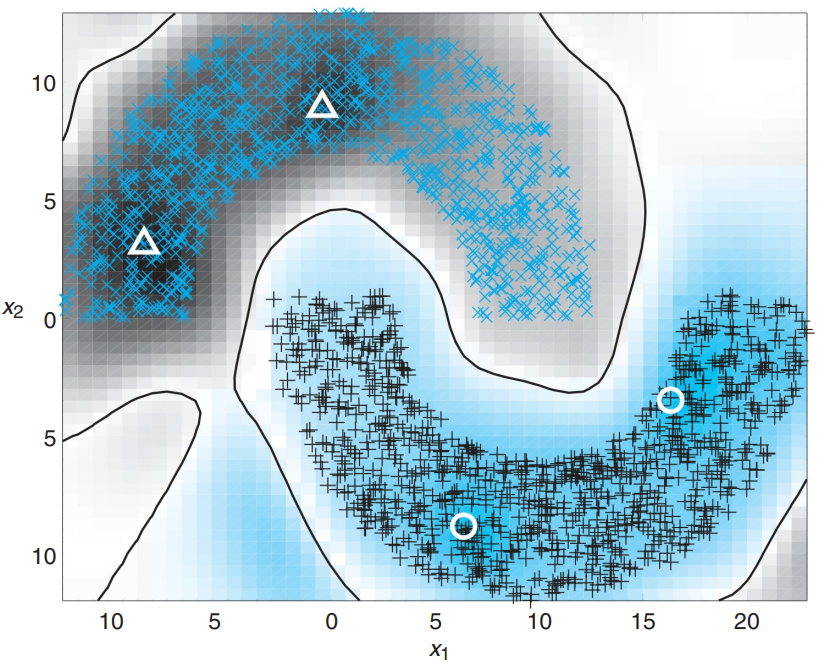
3. Intrinsic regularization parameter $\lambda_I$ = 0.1
파라미터를 0.1까지 증가시킬 경우, 오분류된 샘플 없이 decision boundary가 생성된 것을 확인할 수 있습니다. 이를 통해 $\lambda_I$ 을 증가시킴으로써 unlabeled data에 있는 2개 클래스에 대한 내재적인 정보를 완벽하게 이용하여 모델을 향상시킨 것으로 볼 수 있습니다.
SSL 연구 동향
위 배경지식을 통해 SSL연구에서는 unlabel data로 부터 의미있는 내재적 정보를 추출하기 위해 기존 Supervised learning에 추가적인 정규화 Term을 추가시킨 다는 것을 알아보았습니다. 이러한 내용을 바탕으로 현재 연구되고 있는 SSL core work에 대해 간단히 소개할까 합니다.
1. MixMatch : A Holistic Approach to Semi-Supervised Learning
MixMatch paper는 labeled data 와 unlabeled data에 대해 Entropy Minimization을 적용하여 훈련을 시킵니다. Unlabeled data의 경우 GT(Ground-True) label 이 없기 때문에 Pseudo labeling 기법을 사용합니다. K번의 data augmentation을 적용하여 생성된 입력 값에 대한 모델의 에측 값을 평균값 계산하여 temperature-scaling 기법을 이용하여 sharpening시킨 값을 Soft-label로 활용합니다.

추가적으로 intrinsic regularization term을 위해, unlabeled data를 stochastic property가 있는 Data augmentation 방법론들을 이용해 Augmentation을 진행한 후, 그 데이터에 대한 output이 같도록 강제하는 Consistency Regularization을 사용하였습니다. Augment(x)의 경우 flip 시 probability=0.5 를 설정하여 매번 적용 시 augmented data의 입력 값이 변할 수 있지만, 그 모델의 output은 같도록 만들어 주는 정규화 기법입니다.
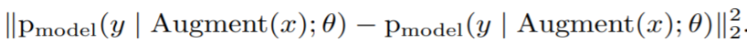
이외, Mixup 이라고 하는 방법론을 이용해 data의 bias를 상대적으로 낮춰줄 수 있는 정규화 기법을 적용하였는데, ERM알고리즘을 이용해 학습된 네트워크가 각 class의 mean prototype에 지나치게 편향되는 경향성을 개선하고 모델을 보다 강건하게 훈련시킬 수 있도록 만듭니다.

Mixmatch를 이용해 50,000장의 training data를 가진 CIFAR-10 에서 오직 250장의 라벨링 이미지로 약 88%의 정확도를 달성하여 다른 기타 모델에 비해 압도적인 성능 변화를 보여주었습니다. 이외에도 SVHN, STL-10 dataset에서 다른 SSL 방법론에 비해 큰 성능차이를 보여주고 있습니다. 표에 표기된 스칼라 값은 Error rate로, 적을 수록 좋은 성능을 의미합니다.
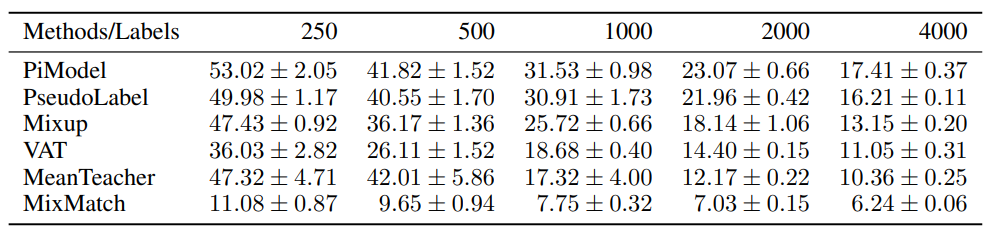

방법론은 비교적(?) 간단하지만, 다양한 메커니즘을 합쳐놓은 방법론이기에 파라미터 튜닝에 대해 상당히 민감하여 데이터셋마다 세심한 파라미터 튜닝을 수행해주어야 한다는 점이 단점으로 생각됩니다.
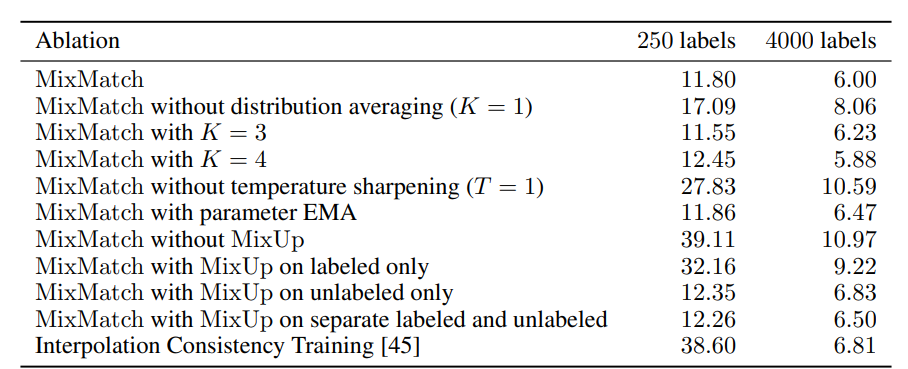
위 연구에 대한 구현 코드는 아래 깃허브를 참고해주세요.
https://github.com/Jeffkang-94/Mixmatch-pytorch-SSL
GitHub - Jeffkang-94/Mixmatch-pytorch-SSL: An unofficial PyTorch implementation of MixMatch - A Holistic Approach to Semi-Superv
An unofficial PyTorch implementation of MixMatch - A Holistic Approach to Semi-Supervised Learning - GitHub - Jeffkang-94/Mixmatch-pytorch-SSL: An unofficial PyTorch implementation of MixMatch - A ...
github.com
2. ReMixMatch : SEMI-SUPERVISED LEARNING WITH DISTRIBUTION ALIGNMENT AND AUGMENTATION ANCHORING
SSL의 접근법들은 Consistency Regularization 과 Entropy minimization 의 방법론으로 통합되어 연구되어 왔으며, 대표적으로 MixMatch가 이 두 개의 cost function을 잘 조합하여 좋은 성능을 달성하였습니다. ReMixMatch에서는 기존 MixMatch Paper에서 제시한 방법론 외적으로, 2가지 추가적인 향상점을 제안합니다.
1. Distribution Alignment
SSL 의 목표는 Labeled data와 Unlabeled data가 모델의 성능 향상을 위해 같이 협업하는 알고리즘 방법론을 찾는 것을 목표로 합니다. 고전적으로 접근하는 방식은 Input-output pair의 mutual information 값을 최대화 시키는 것입니다. 즉, 좋은 분류기일 수록 Input값에 따라 output값이 잘 결정되도록 학습되어야합니다. Classification에서 x 인 input이 주어졌을 때 y 라는 정답 라벨을 알아내는 KL divergence Term은 아래와 같이 표현이 가능합니다. Labeled data의 경우 아래의 식 중 $\mathrm{H}(\mathbb{E}_x[p_{model}(y|x;\theta)])$ 값이 상수이기 때문에 KL을 Optimization관점에서 최소화 시키는 것은 우리가 아는 CrossEntropy Term($-\mathbb{E}_x[H(p_{model}(y|x;\theta)])$ 을 최소화 하는것과 같게 됩니다. 이전의 SSL의 경우 오직 Entropy Minimization관점에서 Unlabeled data를 Pseudo labeling 방법을 통해 CrossEntropy loss를 적용하여 모델을 훈련시켰으나, 앞쪽 Term $\mathrm{H}(\mathbb{E}_x[p_{model}(y|x;\theta)])$ 은 무시되어왔습니다.

그렇다면, 앞 쪽 Term $\mathrm{H}(\mathbb{E}_x[p_{model}(y|x;\theta)])$ 이 의미하는 바가 무엇인가 살펴보겠습니다. 간단히 설명하자면, 앞쪽 Term은 일반적으로 Label이 주어진 경우 True distribution으로써, 모델이 훈련되면서 찾아내야하는 Target distribution이 됩니다. 이 Term은 일반적으로 훈련 데이터가 각 class별로 Uniform distribution을 따른다는 "fairness"를 가정하는데요, 즉 class imbalance 문제가 없다고 가정합니다. 하지만, 실제로 Unlabeled data(marginal distribution $p_x(x)$)의 경우 상당한 class imbalance는 물론 다양한 Outlier들이 훈련을 방해할 수 있습니다. 따라서, RemixMatch paper에서는 running average of prediction을 계속 저장하고 이를 각 class별 prediction으로 나누어주어 label guessing 단계에서 모델이 각 클래스의 불균형 현상을 완화시켜줄 수 있는 방법론을 제시하였습니다. 훈련과정에서 클래스 별 prediction의 running average를 추적하기 때문에 class가 적은 set에 대해서는 normalize된 prediction이 보다 더 큰 contribution을 주는 효과등을 가져올 수 있습니다.
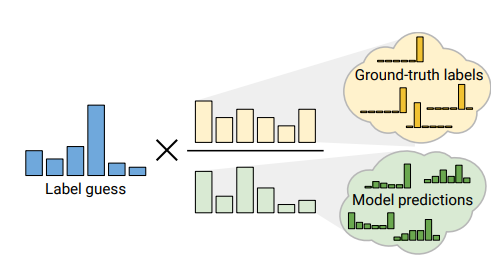
2. Augmentation anchoring
전통적인 augmentation의 경우 Flip, Rotation 등 원본 이미지의 Identity를 크게 훼손하지 않는 선에서 Input에 다양한 stochastic property를 주어 모델을 정규화시키고자 했습니다. 최근에는 CTAugmentation, AutoAugmentation 등 원본 이미지의 identity를 비교적 크게 훼손시키는 "강한" Data augmentation 방법론들이 SSL에 등장하면서, 이를 적용한 consistency regularization의 성능이 크게 향상되었다는 연구 결과가 있었습니다. 전통적인 Augmentation은 "Weak Augmentation", 새롭게 등장한 Augmentation은 "Strong Augmentation" 방법론으로 분류되고 있습니다. 새로운 Augmentation의 방법론을 Mixmatch에 적용해보았지만, 실험 결과상으로 모델이 수렴하지 않는 현상이 발생했습니다. 이는 Mixmatch에서 Strong Augmentation을 적용할 경우 상대적으로 모델의 Logit value가 이상치(Disparate predictions)를 발생할 가능성이 높은데, K Augmentation*을 적용하여 Average 값을 사용하는 기존 훈련법은 이러한 이상치에 상당히 민감하게 반응할 가능성이 높습니다.
*K Augmentation : Mixmatch에서 Stochastic property를 가진(적용할때마다 시간에 따라 output이 달라지는) weak augmentation 방법을 같은 input에 대해 "K"번 적용함. Mixmatch에서는 K=2 일 때 최고의 결과를 얻음. Pseudo label을 생성하기 위해 생성된 Augmented input(K=2) $\{x_1, x_2\}$ 에 대해 Average를 취해 라벨을 획득함
따라서, Remixmatch에서는 Strong Augmentation의 이점을 살리기 위해 Augmentation anchoring이라는 방법론을 도입합니다. 입력 이미지에 대해 Weak Augmentation($W$), Strong Augmentation($S$)을 모두 적용하여 나온 Output, $W(x), S(x)$ 에 대해, $W(x)$ 를 이용해 추론한 Pseudo label을 이용해 $S(x)$에 대한 Entropy Minimization 을 수행합니다. Augmentation Anchoring을 이용해 Mixmatch에 Strong Augmentation을 적용하여 성능을 향상시켰을 뿐 아니라, MSE Loss를 사용해 Logit vector를 CrossEntropy loss로 대체하여 보다 안정적이고 구현을 단순화 시켰습니다. Augmentation 의 경우, Mixmatch 는 K=2 를 사용했지만, ReMixmatch의 경우 K=8일때 가장 좋은 결과를 얻었다고 합니다.
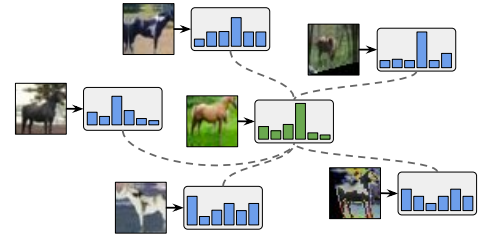
Distribution Alignment 와 Augmentation Anchoring 기법을 활용하여 Mixmatch와 비교해 더 나은 성능을 달성하였습니다.

3. FixMatch : Simplifying Semi-Supervised Learning with Consistency and Confidence
Fixmatch paper는 ReMixmatch 이후 출간된 논문으로, ReMixMatch와 UDA논문의 내용을 결합하여 간단한 SSL 훈련 방법을 소개한 논문입니다. 방법론은 위에서 설명한 논문들의 방법론과 상당히 유사하기에 자세한 설명들은 생략하겠습니다. 아래의 그림처럼 Weak & Strong Augmentation을 정의하고 ReMixmatch에서 소개한 Augmentation Anchoring방법을 사용해 Unlabeled data 에 대한 entropy minimization을 수행합니다.

Pseudo-labeling을 할 때, MixMatch와는 다르게 Sharpening이 아닌 Threshold를 사용하여, 일정 confidence이상의 unlabeled data만이 training에 기여할 수 있도록 조절해주었습니다. 이를 통해 Temeprature T라는 파라미터 값을 없앨 수 있어 SSL훈련 방법을 보다 간단화 시켰습니다. 또한 Unlabeled data가 학습 초기에는 이상치 발생 확률이 높아 Linear lampup이라는 방법을 활용해 unlabeled weight를 점진적으로 증가시켜주는 방법론을 사용했었는데, Fixmatch에서는 Threshold($\tau$) 를 활용한 덕분에 그런 방법론 조차도 없앨수 있게 되었습니다.
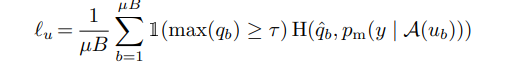
이외, RA, CTA 와 같은 다른 방식의 Strong Augmentation을 사용하여 성능 향상을 이끌어내었습니다.
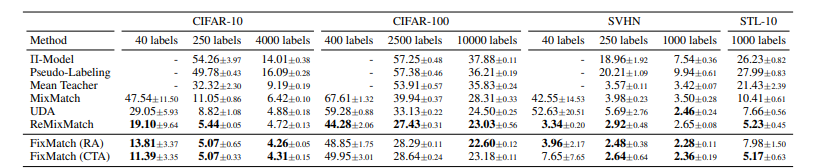
Fixmatch의 경우 앞서 설명한 방법론들을 일부 변경, 또는 간단화시켜 Mixmatch에서 생각했던 파라미터 값들에 대한 성능 변화의 차이가 민감하여 세심한 조절이 필요하다는 단점들을 보완해준 논문입니다. 또한, 이전 연구에서는 시도하지않았던 극심한 환경: 40 labels (각 클래스 별 4개의 데이터만을 Label set으로 활용) 을 가정하여 제안하는 방법론이 더욱 효과적임을 주장하였습니다.

알고리즘에서도 알 수 있듯, Unlabeled data에 대한 weight 값 $\lambda_u$ 값과 threshold $\tau$가 파라미터로 유일하며, 실험 결과상으로 threshold는 큰 성능 변화를 이끄는 민감한 파라미터가 아님이 증명되었습니다. 그 외에도 다양한 optimizer, architecture, lr scheduler등을 통해 ablation study 결과를 제공하고 Implementation detail을 appendix에 자세히 설명해놓았습니다. SSL 연구에 관심있는 분들이라면 한 번씩 읽어보시는것을 적극 추천드립니다.
'Computer Science > 5. Deep learning' 카테고리의 다른 글
| CrossEntropy 와 KL-divergence (4) | 2022.01.23 |
|---|---|
| [Object Detection] Object Detection 튜토리얼 - SSD300 Implementation (0) | 2021.01.11 |
| [Object Detection] Object Detection 튜토리얼 - SSD300 part 2 (0) | 2021.01.11 |
| [Object Detection] Object Detection 튜토리얼 - SSD300 part 1 (0) | 2021.01.08 |
| [Review] Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization (0) | 2019.10.27 |