CrossEntropy와 KL divergence는 Machine Learning에서 가장 많이 접하게 되는 개념들입니다. 요즘 Application level에서의 연구를 하다보니 기본적인 ML지식이 많이 부족한 기분이 들어, 본 포스트에서는 CrossEntropy와 KL divergence에 대한 기본적이고 이론적인 내용을 정리해볼까합니다. 본 내용은 알고있는 내용과 구글에서 블로그를 찾아가며 새롭게 정리한 글임을 알려드립니다.
CrossEntropy
Entropy 란, 주어진 분포 $p(y)$ 에 대한 불확실성(uncertainty)를 나타냅니다. Entropy가 높다라는 것은 주어진 값에 대해 불확실성이 높다라는 의미입니다. 예를 들어, 동전던지기를 통해 앞,뒷면이 나올 확률을 나타내는 분포(예, 베르누이 분포)가 있다고 했을때, 던질때마다 앞면이 나오는 동전의 Entropy는 $H(p) = - 1*log_2(1) = 0$ 이 됩니다. 즉, 앞면이 나오는 상황이 놀랍지 않다는 것이지요. Entropy는 아래의 식으로 정의됩니다.
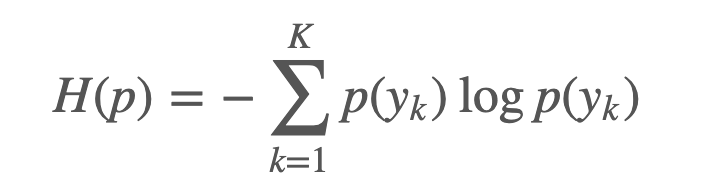
CrossEntropy는 머신러닝에서 주로 Classification 문제에 사용됩니다. 확률 분포가 주어질 때 이 분포가 얼마나 불확실하냐를 측정하는 일종의 메트릭으로서 엔트로피는 사용됩니다. 예를 들어, 다음과 같은 True distribution $p$ 가 주어지고, 이는 현재 날씨를 나타내는 확률이라고 합시다, 이 때 주어진 분포 $p$에 대한 Entropy는 위의 식 정의에 의해 #1.105529 로 계산됩니다. 정보 이론(Information Theory)에서, 이 값은 불확실성을 줄이기 위해 없애야하는 정보의 양을 나타냅니다.
from numpy import log
p = {'rain': .14, 'snow': .37, 'sleet': .03, 'hail': .46}
def entropy(prob_dist):
return -sum([ p*log(p) for p in prob_dist.values() ])
entropy(p)
#1.1055291211185652우리가 만약 random variable에 대한 True distribution(p = {'rain': .14, 'snow': .37, 'sleet': .03, 'hail': .46})
을 알고 있다면 위의 식처럼 entropy를 쉽게 계산할 수 있습니다. 하지만, ML 문제에서 True Distribution은 알 수 없으며, 이 Distribution을 알기 위해 분류기들이 학습을 하는 과정이 ML입니다. ML에서는 True distribution $p(y)$를 알기 위해 $q(y)$ 분포를 이용해 분류기를 학습하게 됩니다.
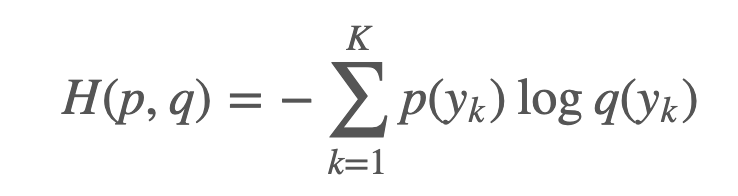
머신러닝 분류기가 $q(y)$를 통해 True distribution $p(y)$을 따를 수 있도록 잘 학습할 수 있게 된다면, 야주 좋은 분류기가 학습될 것입니다. 즉, 좋은 분류기에서는 $H(p,q) \approx H(p)$가 성립하게됩니다.

CrossEntropy와 Entropy와의 차이는 두 확률 분포값의 차이를 의미하며, Kullback-Leibler Divergence, 줄여서 KL Divergence라고 부릅니다.
KL Divergence
KL divergence는 두 분포간의 차이를 정량화하여 나타낼 수 있습니다. 두 분포가 같다면 KL divergence 값은 0이되며, 차이가 있다면 그 값은 항상 양수입니다.
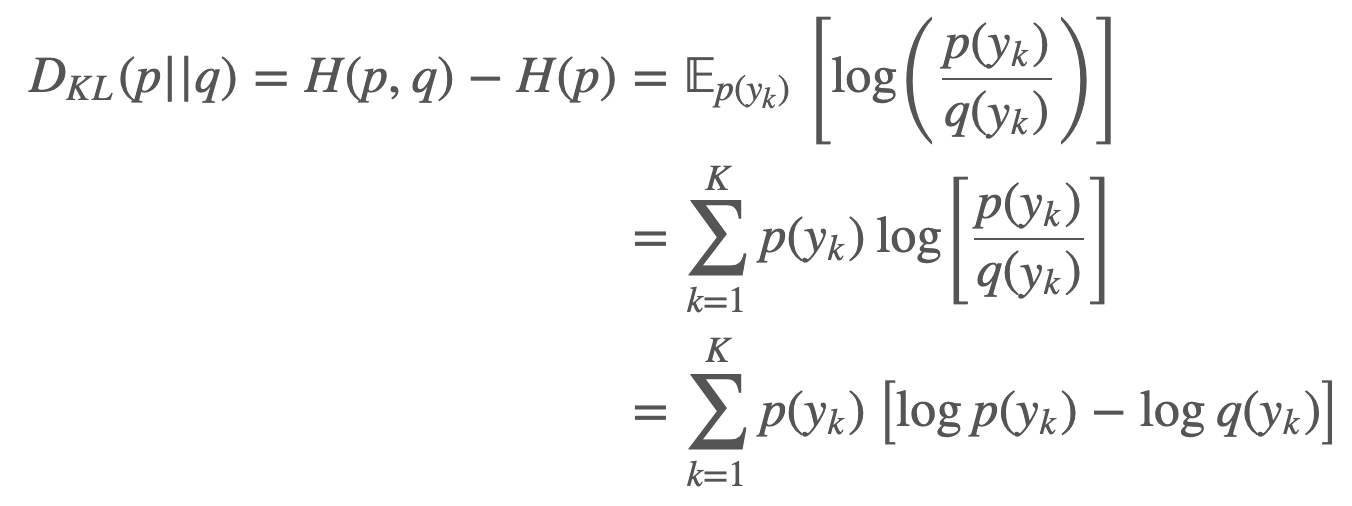
확률분포 $q(y)$ 가 True distribution $p(y)$ 에 가까워질수록 divergence 값은 작아지며, 이는 Cross-entropy 가 하는 것과 동일합니다. 다시말해, KL divergence는 우리에게 2개의 distribution간의 "distance"를 정의하도록 해주는데, 이 "distance"를 최소화 시키는 것은 crossentropy를 최소화하는것과 동일합니다. CrossEntropy를 최소화하는것은 $q(y)$가 $p(y)$에 수렴하는것을 의미하며, 이는 $H(p,q)$가 $H(p)$에 수렴하는것과 같습니다.
CrossEntropy vs KL divergence
KL divergence를 최소화하는 것이 CrossEntropy 를 최소화하는것과 같다는 것이 상당히 모호할 수 있습니다. 아래의 식을 통해 보다 자세히 정리해보겠습니다.
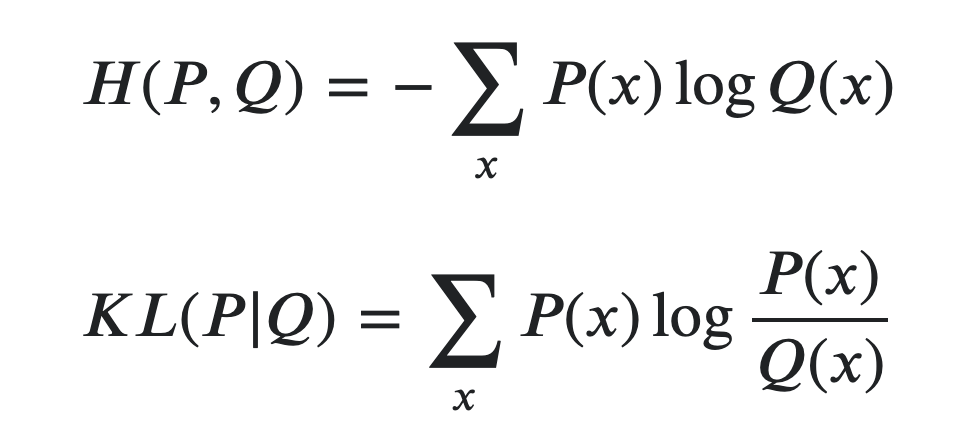
두 개의 수학적 수식은 이론적으로는 다릅니다. KL divergence는 두 개의 확률분포간의 차이를 측정하므로, 예를 들어 $p$ 와 $q$ 가 있다고 가정하겠습니다. 일반적으로, $q$ 는 Neural Network가 예측하는 확률 분포이고, $p$는 Neural Network가 Approximation해야하는 True distribution 입니다. 일반적으로 True distribution은 ML 문제에서 알 수 없는 분포이며, Neural Network를 통해 알아내고자 하는 분포입니다. 따라서, 기본적으로 $H(p)$ 를 모르므로, KL divergence를 바로 Loss term으로 적용할 수 없습니다.
$$D_{KL}(p || q) = P(x)logP(x) - P(x)logQ(x)$$
$P(x)logP(x)$ 는 True distribution이므로 모델의 Parameter값에 대해 변하지 않습니다. 따라서, Loss function 계산시에 상수 값이므로 무시됩니다. Optimization을 수행하는 관점에서 Model의 Parameter값에 의해 영향을 받는 Term은 $-P(x)logQ(x)$ 이며, 이는 CrossEntropy입니다.
요약하자면, True distribution $H(p)$ 가 고정일 때, True distribution을 approximation하기 위한 ML문제는 CrossEntropy를 최소화 시킴으로써 풀 수 있습니다.
'Computer Science > 5. Deep learning' 카테고리의 다른 글
| Semi-Supervised Learning (SSL) 소개 및 동향 (0) | 2021.08.09 |
|---|---|
| [Object Detection] Object Detection 튜토리얼 - SSD300 Implementation (0) | 2021.01.11 |
| [Object Detection] Object Detection 튜토리얼 - SSD300 part 2 (0) | 2021.01.11 |
| [Object Detection] Object Detection 튜토리얼 - SSD300 part 1 (0) | 2021.01.08 |
| [Review] Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization (0) | 2019.10.27 |